Fázový závěs (PLL)

Smyčka fázového závěsu (PLL - Phase-locked loop) pracuje na principu řízení fáze (kmitočtu) napětí přeladitelného a méně stabilního oscilátoru (VCO) oscilátorem přesným a stabilním (krystalový, externí).

Princip funkce PLL

Na výstupu PLL je harmonické napětí V_o, jehož fáze je odvozována od fáze vstupního napětí V_i. Napětí na výstup dodává VCO (Voltage Controlled Oscillator - napětím řízený oscilátor), který je řízen přes smyčku PLL.

Fázový detektor porovnává fázi výstupního napětí V_o s fází vstupního napětí V_i a na jeho výstupu se objevuje rozdílové (chybové) napětí, jehož velikost závisí na rozdílu fází. Po filtraci filtrem (dolní propust), je tímto rozdílovým napětím řízen VCO tak, aby byla fázová odchylka výstupního napětí od vstupního minimalizována.

Významnou roli v obvodu hraje filtr, protože určuje, jak rychle bude fázový závěs reagovat na změny fáze vstupního napětí. Je to dáno tím, že rychlost změn rozdílového napětí odráží rychlost změn fází a podle horní mezní frekvence filtru (dolní propust) budou tyto změny přeneseny na vstup VCO nebo nebudou. Fáze výstupního napětí pak nebude sledovat rychlé změny fáze vstupního napětí.

Figure 1. Fázový závěs

Princip funkce fázového detektoru

Základní princip funkce fázového detektoru spočívá v porovnání fází (a frekvencí) vstupního a výstupního napětí. Výsledkem porovnání je napětí, které slouží k řízení napětím řízeného oscilátoru tak, aby se zkorigovala odchylka fáze výstupního napětí od vstupního. V blokových schématech se používá tento symbol (v obrázku fázového závěsu to ještě musím upravit):

Figure 2. Fázový detektor

Digitální fázový detektor

Je realizování pomocí číslicových obvodů.

Analogový fázový detektor

Je realizován jako násobička napětí. Pozor, ne násobička frekvence! Násobení napětí lze realizovat různými obvody. Jeden z obvodů je známý také jako směšovač, jedná se v podstatě o elektronicky řízený diodový spínač.

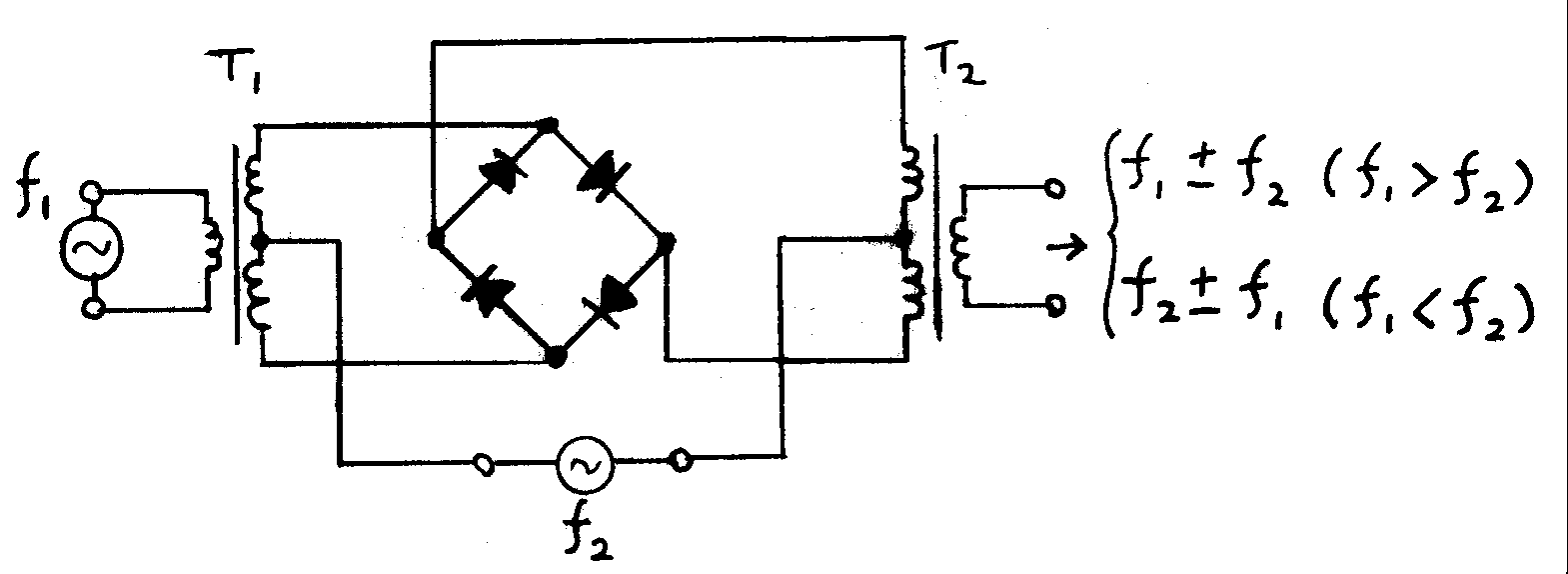
Figure 3. Analogový fázový detektor

Matematický princip funkce fázového detektoru (násobení napětí): Na jednom vstupu bude harmonické napětí o určitém kmitočtu \$u_1(t) = sin (omegat)\$ a na druhém vstupu bude také harmonické napětí o stejném kmitočtu, ale fázově posunuté o úhel \$varphi\$ tedy \$u_2(t) = sin (omegat + varphi)\$. Pro jednoduchost budeme uvažovat, že velikost amplitud je 1.

Na výstupu je pak napětí dané součinem: \$u_1(t) cdot u_2(t) = sin (omegat) cdot sin (omegat + varphi)\$

Využijeme vzorce pro součin dvou funkcí sinus: \$sin alpha cdot sin beta = (cos (alpha - beta) - cos (alpha + beta))/2\$

V našem případě \$alpha = omegat\$ a \$beta = omegat + varphi\$ takže:

\$alpha - beta = omegat - (omegat + varphi) = -varphi\$
\$alpha + beta = omegat + (omegat + varphi) = 2omegat + varphi\$

Napětí na výstupu fázového detektoru pak je:

\$u_1(t) cdot u_2(t) = (cos (-varphi) - cos (2omega t + varphi))/2 = 1/2 cos (-varphi) - 1/2 cos (2omega t + varphi)\$

Vidíme, že napětí na výstupu fázového detektoru má dvě části (pro jednoduchost nebudeme uvažovat konstantu \$1/2\$):

\$cos (-varphi)\$ napětí, jehož velikost je závisí na fázovém posunu mezi napětími \$varphi\$,
\$cos (2omegat + varphi)\$ harmonické napětí, jehož kmitočet je dvojnásobný (\$2omegat\$) oproti původním vstupním napětím.

Složka o dvojnásobném kmitočtu bude odfiltrována dolní propustí ve fázovém závěsu a tak zůstává pouze složka závislá na rozdílu fází a ta řídí VCO.

PLL jako synchronizátor

Synchronizátor je obvod, který je schopen ze vstupního napětí s přesným středním (průměrným) kmitočtem s odchylkami získat tento přesný kmitočet odfiltrováním odchylek.

Jak velké odchylky budou ignorovány závisí právě na nastavení filtru (dolní propusti).

Získání signálu ze šumu: Vstupním signálem může být signál z antény v přijímači, který je velmi slabý a "utopený" v šumu. Fázový závěs je schopen ho ze šumu "vytáhnout".
Odstranění modulace: Modulace je způsob přenosu informace pomocí změn sinusového napětí. PLL je schopen modulaci odstranit a získat tak čisté harmonické (sinusové) napětí, které je dále využitelné v přijímači.

Kmitočet oscilací vysílačů může být řízen přesnými zdroji (GPS apod.) a tak lze pomocí synchronizátoru v přijímači získat z přijímaného signálu velmi přesnou frekvenci.

PLL jako kmitočtová ústředna

Problémem krystalových oscilátorů je, že není možné je přelaďovat, ale kmitočtová ústředna je způsob jak z přesného a stabilního kmitočtu krystalového nebo jiného oscilátoru vyrobit jiný potřebný kmitočet. Toto také označujeme jako frekvenční syntéza. Princip spočívá v použití číslicových děliček v PLL.

Dělička je obvod, který je schopen podělit kmitočet napětí určitým poměrem. Její funkce je založena na funkci čítače. Takže čítač N je dělička 1/N. Dělicí poměr děličky lze číslicově řídit.

Pomocí dělení bychom však získali pouze kmitočty menší než je kmitočet vstupní. Navíc bychom nezískali příliš jemné rozlišení, ale jen kmitočty rovené \$1/2, 1/3, 1/4,...\$. Finta frekvenční syntézy spočívá v použití děliček dvou. Přičemž dělička ve zpětné vazbě PLL (v obrázku označena n) se ve výsledku projeví násobením kmitočtu.

Výsledný kmitočet pak je: \$f = f_(REF) cdot n/m\$

Figure 4. Kmitočtová ústředna

Fázový závěs se chová tak, aby napětí na jeho vstupech měla stejnou fázi (kmitočet). Dělička ve zpětné vazbě PLL (v obrázku označena n) dělí kmitočet výstupního napětí. Kmitočet výstupního napětí je tedy n-krát větší než napětí, které vstupuje do fázového komparátoru.

Nastavováním dělicích poměrů lze vygenerovat velký počet kmitočtů přičemž:

Dělicí poměr n určuje nejvyšší kmitočet, kterého je možné dosáhnout.
Dělicí poměr m určuje nejmenší kmitočet, kterého lze dosáhnout a zároveň, jak jemný je krok "ladění".

Table 1. Výstupní kmitočty pro oscilátor 1 MHz a dvě děličky s dělicím poměrem 1 - 100
Dělicí poměr	Výstupní kmitočet
\$1/100\$	10 kHz
\$2/100\$	20 kHz
\$3/100\$	30 kHz
\$100/1\$	100 MHz

Kmitočtová ústředna se pak chová obdobně jako přeladitelný oscilátor s tím rozdílem, že ladění není plynulé, ale po (jemných) krocích.

Fázový závěs ve formě kmitočtové ústředny je základním prvkem moderních elektronických zařízení, které vyžadují zdroj přesného kmitočtu. Využívá se však i jiným způsobem.